The normal introduction
I’ve been introducing right angled trig to my S3 class this week. I think it’s important that pupils realise that sin, cos and tan are not simply buttons on their calculator. I want them to have a sense of these trig functions as ratios. I don’t spend a lot of time trying to convince them of the wonder of trig through real life applications. I did mention some applications in terms of working out heights of trees etc. More important to me is that pupils appreciate the inherent beauty of trigonometry for it’s own sake rather than some contrived “application”.
In the following paragraph when I say a xo degree triangle, I mean one that has the angle we are concerned with at that size.
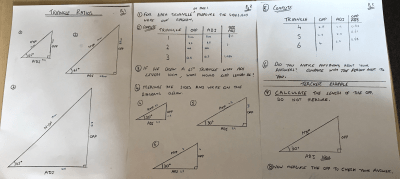
I put together the task below, which I shared on Twitter. This was around identifying through measuring that for a 45o triangle the opposite and adjacent were in a ratio of 1:1. I asked the pupils to use this fact to give me the opposite side when they knew the adjacent side in a variety of triangles. Next, they explored the opposite over adjacent for a range of 30otriangles. Pupils became aware of the fact that in any triangle with an angle of 30o the opposite over adjacent were in the same ratio. They used this value (0.577) to solve simple problems where the adjacent length was known and the opposite unknown. More exploration lead to the value for a 60o triangle and similarly they applied this. I then gave them a mix of questions using 30o, 45o and 60otriangles. I was happy to accept 0.577 rather than the exact value as I felt including surds would confuse matters at this stage.
All of this was went quite well, and when I introduced the trig table of opposite over adjacent values for 1 to 89 pupils began to solve more problems, based upon any angle size in that range. None of this was a new approach to teaching trig for me; I’ve done various activities like this over the years.
During the investigation and the application of these ratio values, the word tan had not been mentioned.
Surprising moments
Quite surprisingly to me, the real excitement and real deep learning in the lesson began to happen when I told them about the tan button on their calculators and how it stored their trig table. They were delighted that they didn’t need to recall all of the values. More interestingly, and the point of this blog, is the questions that the pupils formed for themselves. While I wanted to get on to doing formally laid out examples of applying tan, I decided to allow this opportunity to make space for the conjectures and question the learners were forming.
“If tan30o = 0.577, why can’t we just double it for tan60?o”
This is a common issue with trig in S5/6. I’ve witnessed pupils multiply by two instead of use the double angle formulae. While that level of maths is in the distant future for this class, I thought it interesting that this idea came up. My own understanding and explanation of trig is almost entirely hinged on the graphs and unit circle – neither of which vehicles were available to me when explaining to a class of this age group. I settled, perhaps, unsatisfactorily for an explanation offered by one pupil who simply said “it’s what we could see when we did the measuring and calculations”. The pupil who posed the question seemed satisfied enough by this. I agreed that it does seem counter-intuitive, but hinted that there was more to come in lessons on trig towards the end of S3, where this might make more sense.
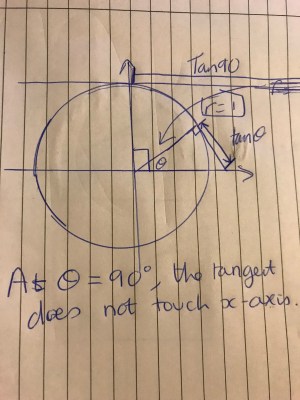
“I tried tan90o on my calculator and it says math error.”
I had asked the pupils to type in tan30 o, tan45o and tan60 o to compare with the values on our trig table. The pupils then took it upon themselves to start trying other values. One of them stumbled upon tan90o and was shocked with what he saw. Now, normally when this happens I have two stock explanations for why tan90 is undefined. i) I refer to sin90 o /cos90 oand talk about division by zero or ii) I talk about tan as being the length of the tangent from the radius to the x-axis on the unit circle. When the radius is rotated to 900 from the horizontal it is no longer possible to know the length of this line, as it never meets the x-axis.
There is a nice applet of the unit circle demonstrating this here.
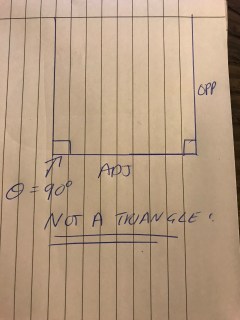
However, with this class who had only just heard the word tan for the first time and had no concept of unit circle, graphs or sin or cos – what could I do? Well, thankfully I didn’t need to do anything. The pupils begin to make conjectures. One girl came out with this incredible bit of insight “we can’t do a 900 degree triangle. That would mean two angles of 900 and no degrees left for the third angle”. I seized upon this and did some demonstration using some sketches like below. I am ashamed to admit – I had never considered this. My own knowledge developed due to the insight of a mathematician 20 years my junior!
“Does it work for values over 90o?”
Another excellent question. This led to pupils trying, without my direction or encouragement, various angles greater than 90oon their calculator. The puzzlement in the air was quite noticeable when they started to get negative values. I asked “what do we notice about these values, is there some pattern?”. Some of them began to make little tables of values… tan 91, tan92, tan 93 etc, Others were more random in their method (or at least appeared to be). Very quickly a consensus emerged that tan91 = – tan89, tan92 = -tan88 etc. The pupils seemed quite captivated by this pattern emerging. I didn’t feel as if I had an adequate explanation without the graphs or unit circle for this phenomenon – but, thankfully, none of them pressed me on this. I promised that they’d understand why this was the case later in S3.
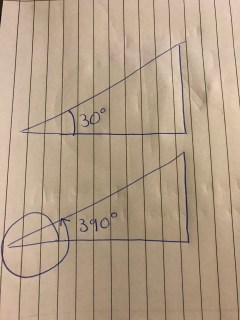
“I tried tan3900 – why is this the same as tan30o?”
Just as I felt that the class had exhausted the wonder and joy they could derive from pressing the tan button on a calculator, one of the pupils posed me the question above. With this, I decided to try a silent explanation. I wanted to let the graphic speak for itself. Have a look at this sketch, which is similar to what I put up….
I then asked if anyone could explain what was happening. The conclusion was reached that after 360o we’d be starting our values all over again. (I didn’t mention 180oat this point). I asked them if there was another occasion when they felt we’d get the same answer as tan3900 and tan30o. More discussion in pairs and trying ideas out – quickly followed by a number of hands suggesting tan750o, much to my absolute joy! The class had led themselves to the knowledge of trig functions being cyclical – something that I’d had no intention of sharing with them at this early stage of their journey.
Conclusion
It is amazing the richness of the discussion that can occur when we allow our pupils to be mathematical. Tacking the shackles off from the lesson-plan and being “in the moment” and reactive with the pupils. I’ve used this quote many times since Danny Brown shared it with me. The very essence of maths teaching is “being mathematical in front of your learners and with your learners”. None of this learning would have happened if I’d stuck to example problem pairs and minimally different questions. Indeed I doubt there would have been very much conceptual learning at all. The inquiry task with the ratios, the opportunities for conjectures opened up a whole learning episode beyond what I had imagined possible. Tomorrow mastering the application of this new knowledge will happen through some drill exercises and some mini whiteboard work, but I feel that this class have a much richer “feel” for trig than any I’ve ever taught at this early stage in their learning. It’s hard to quantify this. A test likely wouldn’t do it, or be fair. Some of these concepts are S4 or s5 level knowledge. And, for most of those older pupils I know they’d be unable to clearly articulate these concepts. This is perhaps one of the flaws of formative assessment. Just because it isn’t easy to identify the learning or whether it has gone in – doesn’t mean the learning hasn’t happened. Nevertheless, I will try and capture more of this knowledge and help the pupils hold onto it by putting some follow up questions in the next few days’ starters.
As always, I welcome questions, criticism and additional ideas on how I can take this forward. Thanks for reading.

I particularly like your \”not a triangle\” diagram, and I think that this is definitely an extension worth spending time on. A few of the others, I'd probably handle with \”ask me again at the end of the lesson!\”. I seem to remember someone (perhaps even you) wrote a post on this exact dilemma in teaching: finding a balance between indulging the children's questions and teaching them material at a level that they can understand.One thing that I'd add to what you've done, is the link between this and similar triangles. Specifically, you can use similar triangles to explain why all triangles with the same angle have the same tangent scale factor. I was reminded of this on my post on this topic (pretty similar to yours!) by a former colleague of mine. http://lukepearce.eu/trigonometry/
LikeLike
Fantastic post, thanks for sharing the detail of what goes on in your classroom. I really like the approach of 1) discovering that the ratio of side lengths is fixed when angle is fixed 2) providing trig tables to work with other angles and only then 3) using the calculator.
LikeLike