Scroll-down for PDF Download



I have tried to scaffold this task so that pupils can work through it independently or in pairs. However, I imagine that a certain amount of whole class practice between pages might be useful with some groups.
The images get harder as the exercises progress.
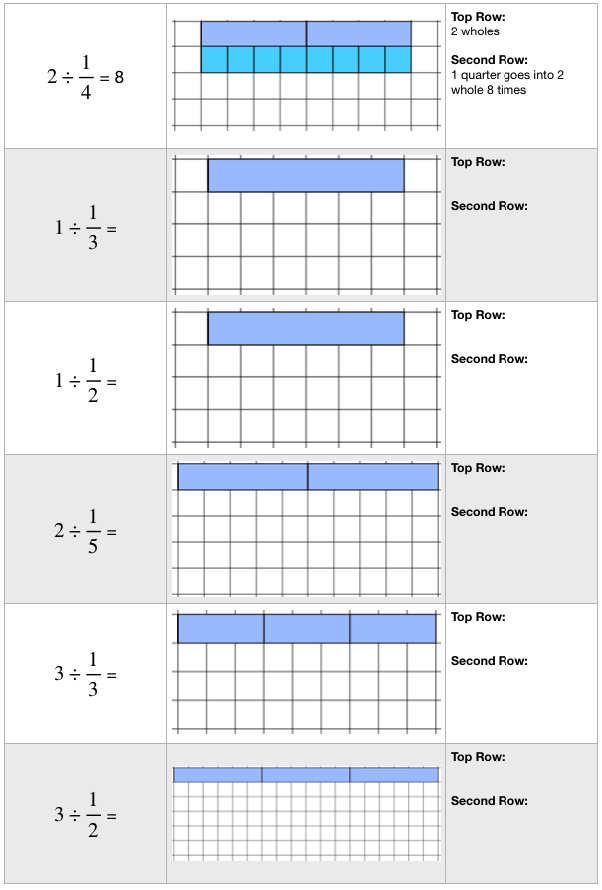
As a pre-requisite pupils need to be familiar with both models of division: partitioning and measurement.
Partitioning: 6 divided by 2 means “share 6 into 2 equal groups of 3.”
Measurement: 6 divided by 2 means “how many times does 2 go into 6?”
Pupils need to have flexibility in their thinking and be able to interchange between these metaphors as appropriate.
As I wrote this task, it occurred to me that division of fractions might be better taught using common denominators as it is some South East Asian countries. In setting up the questions, I had to define the whole as being the lcm of the denominators of the two fractions.
So in the case of 3/4 divided by 2/5 we could write 15/20 divided by 8/20 resulting in 15/8. This is what we’d get using the multiplication by the reciprocal.
Having pupils generate the diagrams from scratch would be a significant step towards this. The relationships between the denominators and number of subdivisions of the whole are the key idea.
Having pupils generate the diagrams from scratch would be a significant step towards this. The relationships between the denominators and number of subdivisions of the whole are the key idea.
Credit: @chrismcgrane84
